テンソル代数
ベクトルの順序対
\( \mathcal{V} \) を体 \( \mathcal{F} \) のベクトル空間であるとする.ベクトルの順序対 \( (\mathbf{a},\mathbf{b}) \) は集合 \( \mathcal{V} \times \mathcal{V} \) ( \( \mathcal{V} \) とそれ自体のデカルト積) に属す.
二階の共変テンソル
二階の共変テンソルは,以下の式で示される \( \mathcal{V} \times \mathcal{V} \) から \( \mathcal{F} \) への関数 \( \mathbf{T}_{\cdot\cdot} \) ( \( \mathbf{T}_{\cdot\cdot} \, \colon \mathcal{V} \times \mathcal{V} \to \mathcal{F} \))として定義される.体 \( \mathcal{F} \) 上の任意の \( \lambda,\mu \) およびベクトル空間 \( \mathcal{V} \) 上の任意の \( \mathbf{a},\mathbf{b},\mathbf{c} \) に対して
\begin{align} &\mathbf{T}_{\cdot\cdot}(\lambda\mathbf{a}+\mu\mathbf{b},\mathbf{c}) = [ \lambda\mathbf{T}_{\cdot\cdot}(\mathbf{a},\mathbf{c})]+[\mu\mathbf{T}_{\cdot\cdot}(\mathbf{b},\mathbf{c})], \tag{2.1} \label{eq:2.1} \\ &\mathbf{T}_{\cdot\cdot}(\mathbf{a},\lambda\mathbf{b}+\mu\mathbf{c}) = [ \lambda\mathbf{T}_{\cdot\cdot}(\mathbf{a},\mathbf{b})]+[\mu\mathbf{T}_{\cdot\cdot}(\mathbf{a},\mathbf{c})], \tag{2.2} \label{eq:2.2} \end{align}
\( \mathbf{T}_{\cdot\cdot} \) は両方の引数についてそれぞれ線形であることを示している.この性質はバイリニア形式(双線形形式)とも呼ばれる.
\( \mathcal{V} \times \mathcal{V} \) における任意の \( (\mathbf{a},\mathbf{b}) \) に対して, \( \mathbf{O}_{\cdot\cdot}(\mathbf{a},\mathbf{b}) \,\colon = 0 \) と定義する.これは二階の共変(唯一の)ゼロテンソルである.
\( \mathbf{T}_{\cdot\cdot}(\mathbf{a},\mathbf{b}) = \mathbf{T}_{\cdot\cdot}(\alpha^{i}\mathbf{e}_{i},\beta^{j}\mathbf{e}_{j}) \, \colon = \alpha^{1}\beta^{1}. \)
二階のテンソルの加算とスカラー乗法
二階のテンソルの加算とスカラー乗算は次の式で定義される.ベクトル空間 \( \mathcal{V} \) の \( \mathbf{a} \) と \( \mathbf{b} \) および体 \( \mathcal{F} \) 上の任意の \( \lambda \) に対して,
\begin{align} [\mathbf{T}_{\cdot\cdot}+\mathbf{G}_{\cdot\cdot}](\mathbf{a},\mathbf{b}) \, &\colon = [\mathbf{T}_{\cdot\cdot}(\mathbf{a},\mathbf{b})]+[\mathbf{G}_{\cdot\cdot}(\mathbf{a},\mathbf{b})], \\ [\lambda\mathbf{T}_{\cdot\cdot}](\mathbf{a},\mathbf{b}) \, &\colon = \lambda[\mathbf{T}_{\cdot\cdot}(\mathbf{a},\mathbf{b})], \\ [-\mathbf{T}_{\cdot\cdot}](\mathbf{a},\mathbf{b}) \, &\colon = -[\mathbf{T}_{\cdot\cdot}(\mathbf{a},\mathbf{b})], \tag{2.3} \label{eq:2.3} \end{align}
\( \eqref{eq:2.3} \) のルールと加算,スカラー乗法および二階の共変ゼロテンソルの定義のもとで, すべての共変テンソルの集合 \( \mathcal{V}^{*} \otimes \mathcal{V}^{*} \) ( \( \otimes \) の定義がされてないのに )はベクトル空間をなす.
[証明]
証明は読者の課題とする.
[証明終わり]
テンソル積 (tensor product)
ふたつの共変ベクトル \( \tilde{\mathbf{u}} \) と \( \tilde{\mathbf{v}} \) との間にテンソル積(tensor product)を定義する.それは次の式であらわされる \( \mathcal{V} \times \mathcal{V} \) から \( \mathcal{F} \) への関数 \( \tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}} \) である.ベクトル空間 \( \mathcal{V} \) の任意の \( \mathbf{a} \) と \( \mathbf{b} \) に対して,
\begin{align} [\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}}](\mathbf{a},\mathbf{b}) \,\colon = [\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{v}}(\mathbf{b})] \tag{2.4} \label{eq:2.4} \end{align}
\( \tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}} \) は 二階の共変テンソルの例であることに注意せよ.
共変ベクトルのテンソル積は次の式を満たす.体 \( \mathcal{F} \) 上の \( \lambda \) とベクトル空間 \( \mathcal{V}^{*} \) 上の任意の \( \tilde{\mathbf{u}},\tilde{\mathbf{v}},\tilde{\mathbf{w}} \) に対して,
\begin{align} \tilde{\mathbf{u}} \otimes (\tilde{\mathbf{v}} + \tilde{\mathbf{w}}) &= [\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}}]+[\tilde{\mathbf{u}} \otimes \tilde{\mathbf{w}}], \tag{2.5} \label{eq:2.5} \\ (\tilde{\mathbf{u}}+\tilde{\mathbf{v}})\otimes\tilde{\mathbf{w}} &= [\tilde{\mathbf{u}} \otimes \tilde{\mathbf{w}}]+[\tilde{\mathbf{u}} \otimes \tilde{\mathbf{w}}], \tag{2.6} \label{eq:2.6} \\ \lambda(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}}) &= (\lambda\tilde{\mathbf{u}}) \otimes \tilde{\mathbf{v}} = \tilde{\mathbf{u}} \otimes (\lambda\tilde{\mathbf{v}}), \tag{2.7} \label{eq:2.7} \\ \tilde{\mathbf{u}} \otimes \tilde{\mathbf{o}} &= \tilde{\mathbf{o}} \otimes \tilde{\mathbf{u}} = \mathbf{O}_{\cdot\cdot}, \tag{2.8} \label{eq:2.8} \end{align}
[\( \eqref{eq:2.5} \) の証明]
\( \eqref{eq:2.5} \) の両側の双一次関数の定義域は同一で \( \mathcal{V} \times \mathcal{V} \) とする.したがって,ベクトル空間 \( \mathcal{V} \) 上の任意のベクトル \( \mathbf{a},\mathbf{b} \) に対して,(2.4)と(1.15)によって以下の式を得る.
\begin{align} [\tilde{\mathbf{u}} \otimes (\tilde{\mathbf{v}}+\tilde{\mathbf{w}})](\mathbf{a},\mathbf{b}) &= [\tilde{\mathbf{u}}(\mathbf{a})][(\tilde{\mathbf{v}}+\tilde{\mathbf{w}})(\mathbf{b})] \\ &= [\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{v}}(\mathbf{b})+\tilde{\mathbf{w}}(\mathbf{b})] \\ &= [\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{v}}(\mathbf{b})]+[\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{w}}(\mathbf{b})] \\ &= [(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})(\mathbf{a},\mathbf{b})]+[(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{w}})(\mathbf{a},\mathbf{b})] \\ &= [(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})+(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{w}})](\mathbf{a},\mathbf{b}). \end{align}
これで \( \eqref{eq:2.5} \) が証明できた.他の式も同様に証明できる.
[証明終わり]
ふたつの共変ベクトル \( \tilde{\mathbf{u}} \) と \( \tilde{\mathbf{v}} \) を次のように定義する.
\begin{align} \tilde{\mathbf{u}}(\mathbf{a}) = \tilde{\mathbf{u}}(\alpha^{i}\mathbf{e}_{i}) \, \colon = \alpha^{1}, \tilde{\mathbf{v}}(\mathbf{b}) = \tilde{\mathbf{v}}(\beta^{j}\mathbf{e}_{j}) \ \colon = \beta^{N}. \end{align}
式(2.4)によって,
\begin{align} [\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}}](\mathbf{a},\mathbf{b}) &= [\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{v}}(\mathbf{b})] = \alpha^{1}\beta^{N}, \\ [\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}}](\mathbf{b},\mathbf{b}) &= \beta^{1}\beta^{N}. \end{align}
共変ベクトルのテンソル積と基底
共変ベクトルのテンソル積 \( \tilde{\mathbf{e}}^{a} \otimes \tilde{\mathbf{e}}^{b} \) を考える.ここで,\( a,b \) は \(1 \) から \( N \) までの値を取るものとする.
共変ベクトルのテンソル積の集合 \( \{ \tilde{\mathbf{e}}^{a} \otimes \tilde{\mathbf{e}}^{b} \} \) (ここで,\(a, b \in \{ 1,\ldots, N \} \) ) は \( \mathcal{V}^{*} \times \mathcal{V}^{*} \) の基底を構成する.
[証明]
線形独立であるかどうかを確かめるため以下のテンソル方程式を考える.
\begin{align} \mu_{ab}[\tilde{\mathbf{e}}^{a} \otimes \tilde{\mathbf{e}}^{b}] = \mathbf{O}_{\cdot\cdot}. \end{align}
式(2.3),(2.4)と(1.16)によって,任意の \( c,d \) に対して以下の式が成り立つ.
\begin{align} [\mu_{ab}(\tilde{\mathbf{e}}^{a} \otimes \tilde{\mathbf{e}}^{b})](\mathbf{e}_{c},\mathbf{e}_{d}) = \mu_{ab}[\tilde{\mathbf{e}}^{a}(\mathbf{e}_{c})][\tilde{\mathbf{e}}^{b}(\mathbf{e}_{d})] = \mu_{ab}\delta^{a}_{c}\delta^{b}_{d} = \mu_{cd} = 0. \end{align}
これは集合 \( \{ \tilde{\mathbf{e}}^{a} \otimes \tilde{\mathbf{e}}^{b} \} \) が線形独立であることを示している.
つづいて展開プロパティを証明するために,以下のような任意のテンソル \( \mathbf{T}_{\cdot\cdot} \) を考える.
\begin{align} \tau_{cd} \,\colon = \mathbf{T}_{\cdot\cdot}(\mathbf{e}_{c},\mathbf{e}_{d}). \tag{2.9} \label{eq:2.9} \end{align}
式(2.1),(2.2),(2.9)により
\begin{align} \mathbf{T}_{\cdot\cdot}(\mathbf{a},\mathbf{b}) &= \mathbf{T}_{\cdot\cdot}(\alpha^{c}\mathbf{e}_{c},\beta^{d}\mathbf{e}_{d}) = \alpha^{c}\beta^{d}\mathbf{T}_{\cdot\cdot}(\mathbf{e}_{c},\mathbf{e}_{d}) \\ &= \tau_{cd}\alpha^{c}\beta^{d}. \tag{2.10} \label{eq:2.10} \end{align}
ここで二階の共変テンソル \( \tau_{cd}(\tilde{\mathbf{e}}^{c} \otimes \tilde{\mathbf{e}}^{d}) \) を考える.式(2.3)と(2.4)により,
\begin{align} [\tau_{cd}(\tilde{\mathbf{e}}^{c} \otimes \tilde{\mathbf{e}}^{d})](\mathbf{a},\mathbf{b}) &= \tau_{cd}[\tilde{\mathbf{e}}^{c}(\mathbf{a})][\tilde{\mathbf{e}}^{d}(\mathbf{b})] \\ &= \tau_{cd}\alpha^{c}\beta^{d}. \tag{2.11} \label{eq:2.11} \end{align}
式(2.10)から(2.11)を引くと,\( \mathcal{V} \times \mathcal{V} \) のすべての順序対 \( (\mathbf{a},\mathbf{b}) \) に対して以下の式を得る.
\begin{align} [\mathbf{T}_{\cdot\cdot} – \tau_{cd}(\tilde{\mathbf{e}}^{c} \otimes \tilde{\mathbf{e}}^{d})](\mathbf{a},\mathbf{b})=0=\mathbf{O}_{\cdot\cdot}(\mathbf{a},\mathbf{b}). \end{align}
ゼロテンソル \( \mathbf{O}_{\cdot\cdot} \) の一意性によって以下の式が成り立つ.
\begin{align} \mathbf{T}_{\cdot\cdot} = \tau_{cd}(\tilde{\mathbf{e}}^{c} \otimes \tilde{\mathbf{e}}^{d}). \end{align}
これは展開プロパティが成り立つことを示している.よって,集合 \( \{ \tilde{\mathbf{e}}^{a} \otimes \tilde{\mathbf{e}}^{b} \} \) は基底である.
[証明終わり]
\( \text{dim} \, (\mathcal{V}^{*} \otimes \mathcal{V}^{*}) = \text{dim} \, N^2. \tag{2.12} \label{eq:2.12} \)
[証明]
証明は明らかなので省略する.
基底変換における二階の共変テンソルの変換規則
式(2.9) に現れる (一意の) スカラー \( \tau_{cd} \) は,二階の共変テンソルの基底 \( \{ \tilde{\mathbf{e}}^{c} \otimes \tilde{\mathbf{e}}^{d} \} \) に関連する \( \mathbf{T}_{\cdot\cdot} \) の成分であると定義する.ここで,\( \mathcal{V} \) の基底を変換した場合の,二階の共変テンソルの成分の変換規則について説明する. (式(1.8)参照)
集合 \( \{ \mathbf{e}_{1},\ldots,\mathbf{e}_{N} \} \) と \( \{ \mathbf{f}_{1},\ldots,\mathbf{f}_{N} \} \) を二つの基底とする.するとこれらは次の変換方程式を満たす.\( \mathbf{f}_{a} = \lambda^{b}_{a}\mathbf{e}_{b}, \ \mathbf{e}_{a} = \mu^{b}_{a}\mathbf{f}_{b}. \)
次に,二階の共変テンソル \( \mathbf{T}_{\cdot\cdot} \) の成分 \( \tau_{cd} \) は,次のように変換される.
\begin{align} \sigma_{ab} &= \lambda^{c}_{a}\lambda^{d}_{b}\tau_{cd}, \\ \tau_{ab} &= \mu^{c}_{a}\mu^{d}_{b}\sigma_{cd} \tag{2.13} \label{eq:2.13} \end{align}
[証明]
式(1.20)を再度記載すると,
\begin{align} \tilde{\mathbf{f}}^{a} = \mu^{a}_{b} \tilde{\mathbf{e}}^{b}, \ \tilde{\mathbf{e}}^{a} = \lambda^{a}_{b}\tilde{\mathbf{f}}^{b}. \end{align}
二階のテンソル \( \mathbf{T}_{\cdot\cdot} \) は次のように表現される.
\begin{align} \mathbf{T}_{\cdot\cdot} = \tau_{cd}\tilde{\mathbf{e}}^{c} \otimes \tilde{\mathbf{e}}^{d} = \sigma_{cd}\tilde{\mathbf{f}}^{c} \otimes \tilde{\mathbf{f}}^{d} \end{align}
式 (1.20) と (2.3) によって,次の式を得る.
\begin{align} \tau_{cd}\tilde{\mathbf{e}}^{c} \otimes \tilde{\mathbf{e}}^{d} &= \sigma_{ab}[(\mu^{a}_{c}\tilde{\mathbf{e}}^{c}) \otimes (\mu^{b}_{d}\tilde{\mathbf{e}}^{d})] \\ &= [\mu^{a}_{c}\mu^{b}_{d}\sigma_{ab}][\tilde{\mathbf{e}}^{c} \otimes \tilde{\mathbf{e}}^{d}] \end{align}
\( \mathbf{T}_{\cdot\cdot} \) の成分の一意性によって以下の式を得る.
\begin{align} \tau_{cd} &= \mu^{a}_{c}\mu^{b}_{d}\sigma_{ab} \end{align}
式 (2.13) のもう一方の式も同様に証明される.
[証明終わり]
\( \mathcal{V} \) を体 \( \mathcal{F} \) の二次元ベクトル空間とする.二つの基底を選定しそれらは以下のように変換されるものとする.
\begin{align} \mathbf{f}_{1} = \mathbf{e}_{2}, \ \mathbf{f}_{2} = -\mathbf{e}_{1}. \end{align}
\( \mathbf{f}_{1} = \lambda^{1}_{1}\mathbf{e}_{1}+\lambda^{2}_{1}\mathbf{e}_{2}, \ \mathbf{f}_{2} = \lambda^{1}_{2}\mathbf{e}_{1}+\lambda^{2}_{2}\mathbf{e}_{2} \) なので,
\begin{align} \lambda^{1}_{1} = 0, \ \lambda^{2}_{1} = 1, \ \lambda^{1}_{2} = -1, \ \lambda^{2}_{2} = 0. \end{align}
よって,\( \mathbf{T}_{\cdot\cdot} \) の成分は次のように変換される.
\begin{align} \sigma_{11} &= \lambda^{c}_{1}\lambda^{d}_{1} \tau_{cd} \\ &= \lambda^{1}_{1} \lambda^{d}_{1} \tau_{1d} + \lambda^{2}_{1} \lambda^{d}_{1} \tau_{2d} \\ &= \lambda^{1}_{1} \lambda^{1}_{1} \tau_{11} + \lambda^{1}_{1} \lambda^{2}_{1} \tau_{12} + \lambda^{2}_{1} \lambda^{1}_{1} \tau_{21} + \lambda^{2}_{1} \lambda^{2}_{1} \tau_{22} \\ &= \tau_{22}, \\ \sigma_{12} &= \lambda^{1}_{1} \lambda^{1}_{2} \tau_{11} + \lambda^{1}_{1} \lambda^{2}_{2} \tau_{12} + \lambda^{2}_{1} \lambda^{1}_{2} \tau_{21} + \lambda^{2}_{1} \lambda^{2}_{2} \tau_{22} \\ &= -\tau_{21}, \\ \sigma_{21} &= \lambda^{1}_{2} \lambda^{1}_{1} \tau_{11} + \lambda^{1}_{2} \lambda^{2}_{1} \tau_{12} + \lambda^{2}_{2} \lambda^{1}_{1} \tau_{21} + \lambda^{2}_{2} \lambda^{2}_{1} \tau_{22} \\ &= -\tau_{12}, \\ \sigma_{22} &= \lambda^{1}_{2} \lambda^{1}_{2} \tau_{11} + \lambda^{1}_{2} \lambda^{2}_{2} \tau_{12} + \lambda^{2}_{2} \lambda^{1}_{2} \tau_{21} + \lambda^{2}_{2} \lambda^{2}_{2} \tau_{22} \\ &= \tau_{11}, \\ \text{det} [\sigma_{ab}] &= \sigma_{11}\sigma_{22} – \sigma_{12}\sigma_{21} \\ &= \tau_{22}\tau_{11} – (-\tau_{21})(-\tau_{12}) \\ &= \tau_{11}\tau_{22} – \tau_{12}\tau_{21} \\ &= \text{det} [\tau_{ab}] . \end{align}
テンソルの転置(transposition)
二階共変テンソル \( \mathbf{B}_{\cdot\cdot} \) の転置 \( {\mathbf{B}_{\cdot\cdot}}^{T} \) は,次の式で定義される.\( \mathcal{V} \times \mathcal{V} \) のすべてのベクトルの順序対 \( (\mathbf{a},\mathbf{b}) \) に対して,
\begin{align} {\mathbf{B}_{\cdot\cdot}}^{T}(\mathbf{a},\mathbf{b}) \,\colon = \mathbf{B}_{\cdot\cdot}(\mathbf{b},\mathbf{a}) \tag{2.14} \label{eq:2.14} \end{align}
対称二階共変テンソル(symmetric second-order covariant tensor)
対称二階共変テンソル \( \mathbf{S}_{\cdot\cdot} \) は,次の式によって定義される.
\begin{align} {\mathbf{S}_{\cdot\cdot}}^{T} = \mathbf{S}_{\cdot\cdot}. \tag{2.15} \label{eq:2.15} \end{align}
そのテンソルの成分は次の式を満たす.
\begin{align} \sigma_{ji} \,\colon = \mathbf{S}_{\cdot\cdot}(\mathbf{e}_{j},\mathbf{e}_{i}) = {\mathbf{S}_{\cdot\cdot}}^{T}(\mathbf{e}_{i},\mathbf{e}_{j}) = \mathbf{S}_{\cdot\cdot}(\mathbf{e}_{i},\mathbf{e}_{j}) = \sigma_{ij}. \tag{2.16} \label{eq:2.16} \end{align}
\( N \times N \) 行列 \( [\sigma_{ij}] \) は対称行列である.これには,\( N+(N − 1)(N/2) = (N(N+1))/2 \) 個の線形独立の成分がある.
次の二階の共変テンソルは対称テンソルである.
\begin{align} \mathbf{S}_{\cdot\cdot} \, \colon = \frac{1}{2}[(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})+(\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}})] . \tag{2.17} \label{eq:2.17} \end{align}
[証明]
\begin{align} \mathbf{S}_{\cdot\cdot}(\mathbf{a},\mathbf{b}) &= \frac{1}{2}[(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})+(\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}})](\mathbf{a},\mathbf{b}) \\ &= \frac{1}{2}[(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})(\mathbf{a},\mathbf{b})+(\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}})(\mathbf{a},\mathbf{b})] \\ &= \frac{1}{2}\{[\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{v}}(\mathbf{b})]+[\tilde{\mathbf{v}}(\mathbf{a})][\tilde{\mathbf{u}}(\mathbf{b})]\} \\ &= \frac{1}{2}\{[\tilde{\mathbf{v}}(\mathbf{b})][\tilde{\mathbf{u}}(\mathbf{a})]+[\tilde{\mathbf{u}}(\mathbf{b})][\tilde{\mathbf{v}}(\mathbf{a})]\} \\ &= \frac{1}{2}\{[\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}}](\mathbf{b},\mathbf{a})]+[\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}}](\mathbf{b},\mathbf{a})]\} \\ &= \frac{1}{2}[(\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}})+(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})](\mathbf{b},\mathbf{a}) \\ &= \mathbf{S}_{\cdot\cdot}(\mathbf{b},\mathbf{a}) \\ &= {\mathbf{S}_{\cdot\cdot}}^{T}(\mathbf{a},\mathbf{b}), \\ \therefore \ {\mathbf{S}_{\cdot\cdot}}^{T} &= \mathbf{S}_{\cdot\cdot}. \end{align}
[証明終わり]
二階反対称共変テンソル(antisymmetric second-order covariant tensor)
二階反対称共変テンソル \( \mathbf{A}_{\cdot\cdot} \) は以下の式で定義される.
\begin{align} {\mathbf{A}_{\cdot\cdot}}^{T} = -\mathbf{A}_{\cdot\cdot}. \tag{2.18} \label{eq:2.18} \end{align}
上記のテンソルの成分は,以下の式を満たす.
\begin{align} \alpha_{ji} = -\alpha_{ij}. \tag{2.19} \label{eq:2.19} \end{align}
これには,\( (N(N-1))/2 \) 個の線形独立の成分がある.
次の二階の共変テンソルは反対称テンソルである.
\begin{align} \mathbf{A}_{\cdot\cdot} \, \colon = \frac{1}{2}[(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})-(\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}})] . \tag{2.20} \label{eq:2.20} \end{align}
[証明]
\begin{align} \mathbf{A}_{\cdot\cdot}(\mathbf{a},\mathbf{b}) &= \frac{1}{2}[(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})-(\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}})](\mathbf{a},\mathbf{b}) \\ &= \frac{1}{2}[(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})(\mathbf{a},\mathbf{b})-(\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}})(\mathbf{a},\mathbf{b})] \\ &= \frac{1}{2}\{[\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{v}}(\mathbf{b})]-[\tilde{\mathbf{v}}(\mathbf{a})][\tilde{\mathbf{u}}(\mathbf{b})]\} \\ &= \frac{1}{2}\{[\tilde{\mathbf{v}}(\mathbf{b})][\tilde{\mathbf{u}}(\mathbf{a})]-[\tilde{\mathbf{u}}(\mathbf{b})][\tilde{\mathbf{v}}(\mathbf{a})]\} \\ &= \frac{1}{2}\{[\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}}](\mathbf{b},\mathbf{a})]-[\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}}](\mathbf{b},\mathbf{a})]\} \\ &= \frac{1}{2}[(\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}})-(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})](\mathbf{b},\mathbf{a}) \\ &= -\frac{1}{2}[(\tilde{\mathbf{u}} \otimes \tilde{\mathbf{v}})-(\tilde{\mathbf{v}} \otimes \tilde{\mathbf{u}})](\mathbf{b},\mathbf{a}) \\ &= -\mathbf{A}_{\cdot\cdot}(\mathbf{b},\mathbf{a}) \\ &= -{\mathbf{A}_{\cdot\cdot}}^{T}(\mathbf{a},\mathbf{b}), \\ \therefore \ {\mathbf{A}_{\cdot\cdot}}^{T} &= -\mathbf{A}_{\cdot\cdot}. \end{align}
[証明終わり]
二階の反変テンソル
二階の反変テンソル \( \mathbf{T}^{\cdot\cdot} \) は \( \mathcal{V}^{*} \times \mathcal{V}^{*} \) から \( \mathcal{F} \) への関数 ( \( \mathbf{T}^{\cdot\cdot} \, \colon \mathcal{V}^{*} \times \mathcal{V}^{*} \to \mathcal{F} \) )で,以下の式であらわされる.体 \( \mathcal{F} \) 上の任意の \( \lambda,\mu \) およびベクトル空間 \( \mathcal{V}^{*} \) 上の任意の \( \tilde{\mathbf{u}},\tilde{\mathbf{v}},\tilde{\mathbf{w}} \) に対して
\begin{align} &\mathbf{T}^{\cdot\cdot}(\lambda\tilde{\mathbf{u}}+\mu\tilde{\mathbf{v}},\tilde{\mathbf{w}}) = [\lambda\mathbf{T}^{\cdot\cdot}(\tilde{\mathbf{u}},\tilde{\mathbf{w}}) ]+[\mu\mathbf{T}^{\cdot\cdot}(\tilde{\mathbf{v}},\tilde{\mathbf{w}}) ], \tag{2.21} \label{eq:2.21} \\ &\mathbf{T}^{\cdot\cdot}(\tilde{\mathbf{u}},\lambda\tilde{\mathbf{v}}+\mu\tilde{\mathbf{w}}) = [\lambda\mathbf{T}^{\cdot\cdot}(\tilde{\mathbf{u}},\tilde{\mathbf{v}}) ]+[\mu\mathbf{T}^{\cdot\cdot}(\tilde{\mathbf{u}},\tilde{\mathbf{w}}) ], \tag{2.22} \label{eq:2.22}\end{align}
関数 \( \mathbf{T}^{\cdot\cdot} \) は双線形である.
\( \mathcal{V}^{*} \) のすべての \( \tilde{\mathbf{u}},\tilde{\mathbf{v}} \) に対して,\( \mathbf{O}^{\cdot\cdot}(\tilde{\mathbf{u}},\tilde{\mathbf{v}}) \,\colon = 0 \) を定義する.これは(唯一の)二階の反変ゼロテンソルである.
\( \mathbf{T}^{\cdot\cdot}(\tilde{\mathbf{a}},\tilde{\mathbf{b}}) = \mathbf{T}^{\cdot\cdot}(\alpha_{i}\tilde{\mathbf{e}}^{i},\beta_{j}\tilde{\mathbf{e}}^{j}) \,\colon = \alpha_{N}\beta_{1}. \)
論理的には,二階の反変テンソルの集合は \( \mathcal{V}^{**} \times \mathcal{V}^{**} \) と書く必要がある.(なぜなら, \( \mathbf{T}^{\cdot\cdot} \, \colon \mathcal{V}^{*} \times \mathcal{V}^{*} \to \mathcal{F} \) なので,\( \mathbf{T}^{\cdot\cdot} \) は \( \mathcal{V}^{*} \times \mathcal{V}^{*} \)の双対空間だからである)ただし,有限次元のベクトル空間 \( \mathcal{V} \) の双対空間の双対空間 \( \mathcal{V}^{**} \) は \( \mathcal{V} \) と同型である(式(1.13)を見よ).したがって,われわれは, \( \mathcal{V}^{**} \times \mathcal{V}^{**} \) を \( \mathcal{V} \times \mathcal{V} \) と表記する.
二階の反変ベクトルの加算,スカラー倍
二階の反変テンソルの加算,スカラー倍などは式 (2.3) とまったく同じになる.このような規則の下で,集合 \( \mathcal{V} \otimes \mathcal{V} \) は次元 \( N^{2} \) のベクトル空間となる.
二階の反変ベクトルのテンソル積
二つのベクトル(反変ベクトル)のテンソル積は,次式のような関数 \( \mathbf{a} \otimes \mathbf{b} \) として定義される.\( \mathcal{V}^{*} \) 上のすべての \( \tilde{\mathbf{u}},\tilde{\mathbf{v}} \) に対して,
\begin{align} [\mathbf{a} \otimes \mathbf{b}](\tilde{\mathbf{u}},\tilde{\mathbf{v}}) \,\colon = [\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{v}}(\mathbf{b})] \tag{2.23} \label{eq:2.23}\end{align}
テンソル積 \( \mathbf{a} \otimes \mathbf{b} \) は 二階の反変テンソルである.\( N^{2} \) 個のテンソル積 \( \{ \mathbf{e}_{a} \otimes \mathbf{e}_{b} \} \) のセットは,\( \mathcal{V} \otimes \mathcal{V} \) の基底を形成する.次の式の線形結合に現れる \( N^{2} \) 個のスカラー \( \tau_{ab} \) は,基底 \( \{ \mathbf{e}_{a} \otimes \mathbf{e}_{b} \} \) に関連する \( \mathbf{T}^{\cdot\cdot} \) の(唯一の)成分である.
\begin{align} \mathbf{T}^{\cdot\cdot} = \tau^{ab}(\mathbf{e}_{a} \otimes \mathbf{e}_{b}) \tag{2.24} \label{eq:2.24}\end{align}
基底ベクトルが次のように変換される場合
\begin{align} \mathbf{f}_{a} = \lambda^{b}_{a}\mathbf{e}_{b}, \ \mathbf{e}_{a} = \mu^{b}_{a}\mathbf{f}_{b}, \end{align}
二階の反変テンソル \( \mathbf{T}^{\cdot\cdot} \) の成分は,次のように変換される.
\begin{align} \sigma^{ab} = \mu^{a}_{c}\mu^{b}_{d}\tau^{cd}, \ \tau^{ab} = \lambda^{a}_{c}\lambda^{b}_{d}\sigma^{cd} \tag{2.25} \label{eq:2.25}\end{align}
二階の混合テンソル
つづいて混合テンソルを定義する.
\begin{align} \mathbf{T}^{\cdot}_{\ \cdot} \,\colon \mathcal{V}^{*} \times \mathcal{V} \to \mathcal{F}, \\ \mathbf{T}^{\ \cdot}_{\cdot}\,\colon \mathcal{V} \times \mathcal{V}^{*} \to \mathcal{F}, \end{align}
すべての \( \tilde{\mathbf{u}} \) とすべての \( \mathbf{b} \) に対して,
\begin{align} \mathbf{O}^{\cdot}_{\ \cdot}(\tilde{\mathbf{u}},\mathbf{b}) \,\colon = 0 \tag{2.26} \label{eq:2.26} \end{align}
すべての \( \mathbf{a} \) とすべての \( \tilde{\mathbf{v}} \) に対して,
\begin{align} \mathbf{O}^{\ \cdot}_{\cdot}(\mathbf{a},\tilde{\mathbf{v}}) \,\colon = 0 \tag{2.27} \label{eq:2.27} \end{align}
を定義する.これは(唯一の)二階の反変ゼロテンソルである.これらは二階の混合ゼロテンソルと呼ばれる.
恒等混合テンソル \( \mathbf{I}^{\cdot}_{\ \cdot} \) と \( \mathbf{I}^{\ \cdot}_{\cdot} \) を次のように定義する.
\begin{align} &\mathbf{I}^{\cdot}_{\ \cdot}(\tilde{\mathbf{e}}^{a},\mathbf{e}_{b}) \,\colon = \delta^{a}_{b}, \tag{2.28} \label{eq:2.28} \\ &\mathbf{I}^{\ \cdot}_{\cdot}(\mathbf{e}_{a},\tilde{\mathbf{e}}^{b}) \,\colon = \delta^{b}_{a}. \tag{2.29} \label{eq:2.29} \end{align}
これによって次の式を得る.
\begin{align} \mathbf{I}^{\cdot}_{\ \cdot}(\alpha^{a}\tilde{\mathbf{e}}^{a},\beta^{b}\mathbf{e}_{b}) = \alpha_{a}\beta^{b} = \mathbf{I}^{\ \cdot}_{\cdot}(\beta^{a}\mathbf{e}_{a},\alpha_{b}\tilde{\mathbf{e}}^{b}). \end{align}
混合テンソルのテンソル積
混合テンソルのテンソル積を次のように定義する.すべての \( \mathbf{a},\mathbf{b} \) およびすべての \( \tilde{\mathbf{u}},\tilde{\mathbf{v}} \) に対して,
\begin{align} &[\mathbf{a} \otimes \tilde{\mathbf{v}}](\tilde{\mathbf{u}},\mathbf{b}) \,\colon = [\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{v}}(\mathbf{b})], \tag{2.30} \label{eq:2.30} \\ &[\tilde{\mathbf{u}} \otimes \mathbf{b}](\mathbf{a},\tilde{\mathbf{v}}) \,\colon = [\tilde{\mathbf{u}}(\mathbf{a})][\tilde{\mathbf{v}}(\mathbf{b})]. \tag{2.31} \label{eq:2.31} \end{align}
混合テンソルの基底
集合 \( \{ \mathbf{e}_{a} \otimes \tilde{\mathbf{e}}^{b} \} \) と集合 \( \{ \tilde{\mathbf{e}}^{a} \otimes \mathbf{e}_{b} \} \) はそれぞれ \( \mathcal{V} \times \mathcal{V}^{*} \) と \( \mathcal{V}^{*} \times \mathcal{V} \) の基底である.\( N^{2} \) 次元のベクトル空間 \( \mathcal{V} \otimes \mathcal{V}^{*} \) と \( \mathcal{V}^{*} \otimes \mathcal{V} \) は同型(isomorphic)である. ふたつの基底間の変換は,いままでよくでてきた次の方程式によって提供されるとする.
\begin{align} \mathbf{f}_{a} = \lambda^{b}_{a}\mathbf{e}_{b}, \ \mathbf{e}_{a} = \mu^{b}_{a}\mathbf{f}_{b}. \end{align}
次に,混合テンソル \( \mathbf{T}^{\cdot}_{\ \cdot} \) および \( \mathbf{T}_{\cdot}^{\ \cdot} \) の成分は次のように変換される.
\begin{align} &\sigma^{a}_{b} = \mu^{a}_{c}\lambda^{d}_{b}\tau^{c}_{d}, \ \tau^{a}_{b} = \lambda^{a}_{c}\mu^{d}_{b}\sigma^{c}_{d}, \tag{2.32} \label{eq:2.32} \\ &\sigma^{b}_{a} = \lambda^{c}_{a}\mu^{b}_{d}\tau^{d}_{c}, \ \tau^{b}_{a} = \lambda^{c}_{a}\mu^{b}_{d}\sigma^{d}_{c}. \tag{2.33} \label{eq:2.33} \end{align}
\( \mathcal{V} \,\colon = \mathbb{R}^{2}, \ \tilde{\mathbf{u}}(\alpha^{1},\alpha^{2}) \,\colon = \alpha^{2} \) および \( \tilde{\mathbf{v}}(\beta^{1},\beta^{2}) \,\colon = \beta^{1} \) と定義する.
\( \mathcal{V} \otimes \mathcal{V}^{*} \) の混合二階テンソル \( (\alpha^{1} , 2) \otimes \tilde{\mathbf{v}} \) のクラスを考える.\( \mathcal{V}^{*} \times \mathcal{V} \) の成分 \( (\tilde{\mathbf{u}},(-2^{-1},\beta^{2})) \) に対する関数 \( (\alpha^{1},2) \otimes \tilde{\mathbf{v}} \) の値を計算してみる.式(2.30) より以下の式を得る.
\begin{align} [(\alpha^{1},2) \otimes \tilde{\mathbf{v}} ](\tilde{\mathbf{u}}(-2^{-1},\beta^{2})) = [\tilde{\mathbf{u}}(\alpha^{1},2)][\tilde{\mathbf{v}}(-2^{-1},\beta^{2}))] \equiv (2)(-2^{-1}) = -1. \end{align}
練習問題
\( \mathcal{V} \) を \( 4 \) 次元の実ベクトル空間とする.またつぎの行列はひとつの基底変換の表現行列である.
\begin{align} &[\lambda^{a}_{b}] =\begin{bmatrix} \cosh{\beta} & 0 & 0 & -\sinh{\beta} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\sinh{\beta} & 0 & 0 & \cosh{\beta} \end{bmatrix}. \end{align}
\( \mathbf{F}_{\cdot\cdot} = \phi_{ab}\tilde{\mathbf{e}}^{a} \otimes \tilde{\mathbf{e}}^{b} \) を反対称テンソルとする場合,上記の行列で変換された成分 \( \phi^{*}_{ab} \) を求めよ.
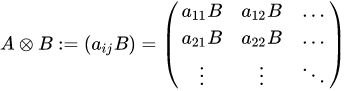
コメント