単射の定義
\begin{align} x_1 \ne x_2 \implies f(x_1) \ne f(x_2) \end{align}
または
\begin{align} f(x_1) = f(x_2) \implies x_1 = x_2 \end{align}
全射の定義
任意の \( y \in Y \) に対して,ある \( x \in X \)が存在して, \( f(x) = y \)
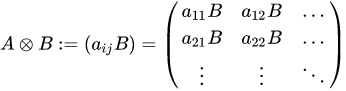 algebra
algebra\begin{align} x_1 \ne x_2 \implies f(x_1) \ne f(x_2) \end{align}
または
\begin{align} f(x_1) = f(x_2) \implies x_1 = x_2 \end{align}
任意の \( y \in Y \) に対して,ある \( x \in X \)が存在して, \( f(x) = y \)
コメント